产生混叠的来源:这一点在奈奎斯特定理中给出了说明。奈奎斯特定理指出:时间连续信号转换成离散信号时,需要在一个周期内的采样次数多于 2 次。如果采样次数不够,将无法恢复丢失的信息。从图 1 可以更清晰地看到这一点,如果信号每周期采样一次,得到的只是一个直流信号(幅度为任意值),如图 1a 所示。如果每周期采样两次,得到一个方波信号(图 1b)。值得注意的是:对输入信号进行每周期 2 次的采样是一种非常特殊的情况,任何时候都要避免这种情况。图 1c 所示是以 200kHz 采样率对 190kHz 信号进行采样的情况。所得信号是一个完好的正弦波,但频率是错误的。频率的改变正是由于混叠现象导致的。
图 1a. 对正弦信号进行每周期一次的采样时,得到一个幅度为任意值的直流信号。
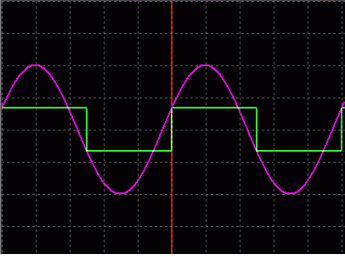
图 1b. 对同一正弦波每周期采样两次,得到一个方波,幅度信息丢失。
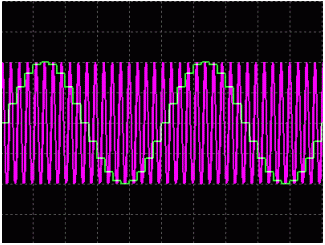
图 1c. Fsignal = 190kHz、Fs = 200kHz 是欠采样信号,所得结果是混叠现象导致的。
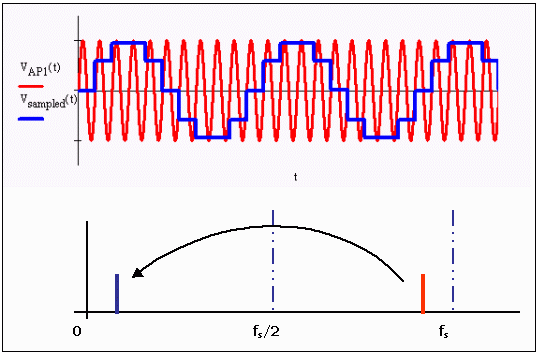
图 2 所示是在频域的表现形式,从图中可以看出,频率高于 f ≥ fs/2 的信号被镜像到 fs/2。为了避免这种现象,必须保证信号中没有更高的频率成份。因此,我们必须了解信号的最高频率,采样频率需要高于这个频率的两倍。一种最原始的考虑是从数字域解决这个问题,但这显然是不可取的,因为一旦完成信号采样,有些信号混叠到所感兴趣的频段,则无法从信号中移除这些频率成份。抗混叠滤波必须在模拟域进行,即在信号采样之前。
图 2. 频域中的混叠现象,欠采样信号镜像到 fs/2。
下一步 — 设计抗混叠滤波器。设计抗混叠滤波器需要首先确定所希望的滤波特性(截止频率、过渡带衰减等),然后选择能够满足应用需求的最佳滤波方案(有时称为滤波器类型)。一般情况下,采用过采样、而且过采样频率越高,滤波器设计越容易。但是,过采样需要更高速率的 ADC,成本也越高。
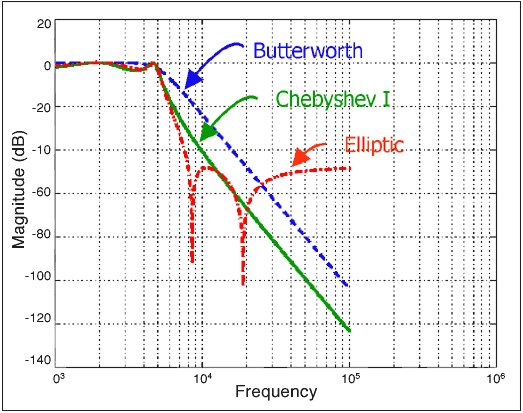
例如,过采样因子为 8 时,采样频率是最高信号频率的八倍。这在 ADC 成本和滤波器复杂度方面达到了一个较好的折衷。假设 ADC 分辨率为 14 位,能够提供 80dB 的信噪比(SNR)。采用一半的采样率(这里为信号频率的 4 倍)时,低通滤波器需要提供 80dB 的衰减,以确保所有杂散信号经过足够的衰减,不会出现在采样后的信号中。这意味着在过渡带内需要提供每倍频程 40dB 的衰减,需要高阶滤波器达到这一设计要求。7 阶巴特沃斯滤波器能够满足上述要求,但对于具体应用并非最佳选择。可针对不同的应用选择不同的滤波器类型,图 3 所示为巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器的频响特性。从图中可以看出,它们具有不同的通带、过渡带特性。椭圆滤波器与巴特沃斯滤波器相比,椭圆滤波器的过渡带更陡峭,但其相频特性较差。应根据具体应用选择滤波器类型,对于普通的数据采集系统,可以选用巴特沃斯滤波器(或贝塞尔滤波器),如果对相位精度要求不高的话,也可以选择切比雪夫、甚至椭圆滤波器。
图 3. 不同滤波器频率响应的比较
通用的 A/D 转换器有:用于中等速率的 SAR (逐次逼近) ADC;用于高速到超高速率的闪速 ADC;用于低速系统的Σ-Δ ADC。它们都需要抗混叠滤波器,对滤波器的要求取决于转换速率、所希望的输入带宽,但Σ-Δ ADC 比较特殊。这种转换技术采用非常高的输入采样率和转换速率,而后续数字滤波降低了有效吞吐率,这会影响分辨率(动态范围)的提高。Σ-Δ ADC 对抗混叠滤波器的要求与输入采样率和最高信号频率之比有关,这种对需求的降低同样也表现在其它过采样数据转换器中,这种情况下可以选用简单的 RC 滤波器。选用较简单的抗混叠滤波器会产生较长的传输延时,这为使用闭环控制或多路转换的转换器增加了设计难度。
由于模拟滤波器具有一定的设计难度和较大的公差,而且制造困难,特别是对于空间紧凑的产品,许多设计人员不愿意使用模拟滤波器。衡量误差的一个较好准则是假设分离元件容限加倍,这样,如果采用标准的商用化电阻器和电容器,将对角频率和过渡带造成很大的误差。解决这一问题的最佳途径是选择集成滤波器方案,可以从 Maxim 等公司获得这种芯片。
集成滤波器有两种类型:连续时间滤波器和开关电容滤波器,连续时间滤波器通常需要外部元件调节角频率,从而限制了它们的灵活性。开关电容滤波器可以根据其结构灵活使用,一般情况下,可以替代分离或集成连续时间滤波器。
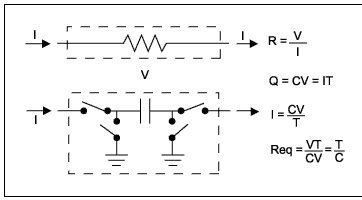
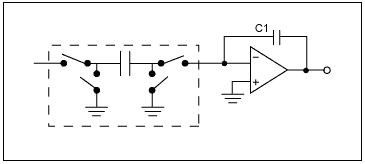
开关电容滤波器是一种很早就被人们认可的滤波器结构,利用当前的硅工艺技术能够可靠集成。其工作原理和数学推导如图 4 所示。工作原理是:在电容器两端的开关控制下,电容被充电、放电。这种电荷转移过程产生脉冲电流,可以计算其平均电流,当开关频率足够快时,该电流等效于流过电阻的电流,可看作是电阻被一个电容所取代。电流和间接电阻值取决于两个因素:电容大小和开关频率。开关频率越高、电容值越大,则电流越大,或者说,电阻值越小。如果采用这种滤波器结构,频率特性将随着电容尺寸或开关频率的变化而改变。在集成方案中,电容值是固定的,滤波特性受开关频率的控制。这种滤波器的原理如图 5 所示。
图 4. 开关电容原理框图
图 5. 利用开关电容技术构成简单的滤波器
滤波器的精度取决于各个元件的容限,分离方案中,我们只能使用容限不一致的元件。而在集成方案中,可以保证很高的元件一致性(0.1%以内)。因此,我们可以很好地控制集成滤波器的频响特性。例如,MAX7490 的角频率精度可以达到 0.2%,而采用分离元件则无法达到这一指标。另外,集成方案还具有出色的温度特性,温漂系数可以达到 10ppm/°C。
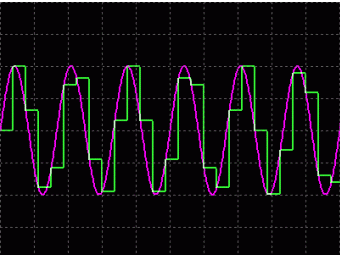
这里还需要特别指出开关电容方案对信号的采样,它将时间连续信号转换成时间离散信号,这意味着我们还要再次考虑混叠问题。值得庆幸的是,这种滤波器的采样速率非常高,通常是 100 倍的过采样。所以,只需采用一个简单的阻容滤波器。系统中另外一个需要考虑的问题是:开关时钟的相位抖动所产生的失真,这与 ADC 中存在的问题相同。图 6 给出了一个正确信号被错误采样的情况,会导致一定的幅度误差。
图 6. 欠采样引起的幅度失真
时钟抖动有两种表现形式,如果相位误差是随机的,噪声基低将升高;如果抖动是周期性的,失真(THD)将增大。抖动是一个时间量,例如:ps 峰峰值或 RMS。为了达到一定的信号纯度,能够容许多大的抖动呢? 参考文献 1 中指出,对于一个 16 位的系统,1nspp (峰峰值)的时钟抖动会使 SNR 从 98dB 降至 91dB。为了将抖动的影响限制到 0.5dB,抖动不能高于 400pspp。
利用商用化的时钟振荡器可以很容易地满足上述抖动指标的要求,如:SaRonix NTH5,抖动只有 8psRMS (53pspp)。这种方案的缺陷是限制了信号频率。大多数系统中,其它器件(如 ADC、μC、等)也需要提供时钟。如果这些时钟用其它振荡器产生,这些时钟将不同步,将会引起其它诸多问题。MAX7375 或 DS1085 能够产生多个时钟,而且彼此同步,并可提供较好的抖动指标(分别为 160ps 和 300ps),可以达到 90dB 以上的信号纯度。利用这种器件提供时钟的另一个好处是:可编程不同的时钟频率。也就是说,可以获得具有软件可编程频率响应特性的模拟滤波器,从而创建一个极其灵活的系统。
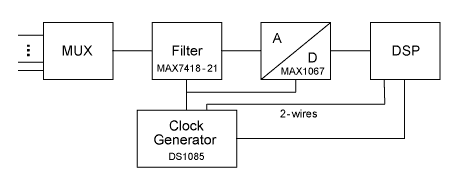
图 7 是基于上述讨论提供的一个数据采集系统方案。ADC 具有 14 位分辨率和 200ksps 采样率(MAX1067 系列)。该器件每次转换至少需要 24 个时钟。抗混叠滤波器采用了 MAX7418-21 系列产品,该系列滤波器提供各种滤波器类型,如贝塞尔、巴特沃斯、椭圆等。角频率设置为 1/100 fClk。考虑到 DSP 控制转换器的采样(只需要一个定时器),同一时钟可以用于滤波器和 ADC,完全同步。利用 DS1085 产生时钟,能够得到两路时钟,第二路时钟可用于 DSP。DS1085 通过 2 线接口编程,当系统工作在不同的采样速率时可以重新设置频率,用同一块 PCB 实现不同的功能。
图 7. 数据采样系统原理框图
图 7 所示电路,器件之间协同工作,在成本和复杂程度上都是可以接受的。另外一个优势是可编程性,提供了极大的灵活性,既简化了设计,也降低了成本。





 猜你喜欢
猜你喜欢
 行业资讯
行业资讯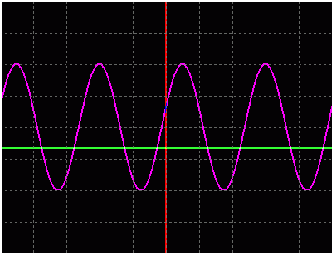
 询价
询价